1. 引子
近几年开设《初等数论》课程, 我总是要抽出一定的时间专门给学生科普一下关于素数的故事. 这篇科普文章正是基于讲稿整理出来的.
素数是整个数论的灵魂。然而多数学生对素数的了解非常少. 很多人不明白:为什么我们要研究素数?素数为何与众不同? 素数到底有趣在哪里? 素数对数学很重要吗? …… 如果学生在上完一个学期的数论课后,却仍然对素数茫然无知,那无疑是一种讽刺—这就好比你看完一场戏,却不知道主角做了些什么.
写这篇文章的另一目的也是为了给那些依然执着于证明哥德巴赫猜想的民科们做一次扫盲的尝试—尽管他们中的大多数会继续执着下去。然而我们不得不承认这样一个现实:民科们对素数的热情与执着确实远远超过很多数学系的本科生—这多少会让老师们感到沮丧.
2. 素数有多少?
我们说一个整数a 能被另一个整数b 整除, 就是指![]() 是整数. 我们也把b称作a的因子.
是整数. 我们也把b称作a的因子.
一个素数 (Prime)是指这样一种正整数: 除了1 和它本身之外, 其它任何正整数都不可能整除它. 我们也可以这么定义素数: 它不能写成两个大于1 的整数的乘积. 有时我们也将素数称作质数. 通常我们不承认1 是素数. 这样做的好处下面会介绍. 除了1 和素数之外, 其他的正整数统称为合数.
最初的几个素数是2, 3,5,7,11,……. 显然6 不是素数, 因为6=2*3. 所有的素数中只有2 是偶数! 这件看似平凡的事, 其实很重要. 在许多数学研究中, 2 和其他素数会对我们所考虑的问题产生不同的影响.
你可能会问, 为什么我们把这样的数命名为”素数”? 这实际上来自于素数最基本的结论 (算术基本定理):
任何大于1 的正整数n都可以唯一地分解成一些素数的乘积 n = p1 p2…ps,这里p1≤ p2≤…≤ ps 都是素数 (允许相同).
无论如何, 素数本身不能再进一步分解成一些更小的正整数乘积, 因此它在此意义下是最基本的数—类似于朴素的原子论—从而命名它们为“素数”或者“质数”.容易看到, 假如我们承认1 是素数, 那么算术基本定理就不能保证分解是唯一的了, 因为1 可以写为任意多个自身的乘积.
接下去,一个最自然不过的问题当然是: 究竟有多少素数?无限多个还是仅有有限个?这个问题的答案早由欧几里德在两千多年前解决了. 他用初等方法巧妙地证明:存在无限多个素数. 具体言之, 我们假设所有正整数中只有有限个素数p1, p2,…, pn, 那么可以构造一个正整数
N = p1p2…pn+1.
你很容易发现, 左边的N 分解成素数乘积的话, 不可能包含任何素数pi , 因此它的分解式中必定含有这些pi之外的新素数. 这就和我们的假设矛盾!
这个证明包含了富有启发性的思想. 事实上, 证明本身并没有提供构造出所有素数的具体方法. 但是它却能告诉我们素数有无限个! 这就是数学中所谓的“存在性证明”:它告诉你某些对象存在,但是却没有具体构造出来. “存在性”是数学哲学中的一个深刻话题, 涉及到数学大厦的根基。 数学史上曾经关于这类问题有过广泛而激烈的争论, 有人反对这种类型的证明,有人却支持它们. 这场争论涉及了许多重要的数学家—比如希尔伯特等等‐‐产生了许多和数学、逻辑、哲学相关的理论. 有兴趣的读者可以参考相关文献, 我们不再赘述.
类似欧几里德的证明, 你也可以轻松断言:所有被4 除余数为3 的素数有无限个! 换言之, 就是等差数列3,7,11,15,19,…中包含无穷多个素数. 这就产生了一个有趣的问题:
一个等差数列 a, a+b, a+2b, ……, a+nb, …… 中是否包含无限个素数?
数学家狄利克雷回答了这一问题 (狄利克雷定理):
假如a 和b 不能同时被一个大于1 的正整数整除, 那么答案是肯定的!
不要以为欧几里德的方法可以轻松解决这一问题。 事实上, 除了少数情形之外,这个问题是不可能用它来解决的.
如果我们把等差数列换成其他数列, 结论会怎样呢? 比如考虑以下的数列:
2,5,10,17, 26,…,n2 +1,…
其中是否有无限多个素数呢? 让人颇为失望的是, 这至今仍是一个未解决的难题.
3.素数是怎么分布的?
知道“素数有无限多个”仅仅是个开始. 我们还想知道更多! 比如, 素数在所有自然数所占的比率多大? 当然,我们首先要说明, “比率”在这里意味着什么. 对任何正实数x, 我们用π(x) 表示不超过x的素数的个数. 比如π(1) = 0 ,π(4) = 2 , π(2.5) = 1 等等. 我们用![]() 来反映所有不超过x 的正整数中, 素数所占的比率—也称作平均分布密度. 一个简单的结论告诉我们: 当x 非常非常大时,
来反映所有不超过x 的正整数中, 素数所占的比率—也称作平均分布密度. 一个简单的结论告诉我们: 当x 非常非常大时, ![]() 几乎就等于0. 换句话说, 素数在所有正整数中极为罕见, 可以说少得几乎没有—尽管我们知道它们有无穷多个!这就好比宇宙中有生命的星球也许有无限多个, 但是它们相隔得太远, 相对整个宇宙来说实在是十分稀疏罕见的.
几乎就等于0. 换句话说, 素数在所有正整数中极为罕见, 可以说少得几乎没有—尽管我们知道它们有无穷多个!这就好比宇宙中有生命的星球也许有无限多个, 但是它们相隔得太远, 相对整个宇宙来说实在是十分稀疏罕见的.
对一般人来说,这个结论似乎已经让我们走到了问题的尽头. 但是天才数学家高斯却不这么认为. 在那个没有计算机的年代, 他通过大量的手工计算, 单凭超人的直觉,竟然得到了一个让人吃惊的猜测 (但其本人并未证明):
当x 非常大时,素数出现的比率![]() 约等于
约等于![]() , 换言之,
, 换言之,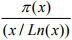 约等于1.
约等于1.
这里Ln(x)是x的对数函数. 高斯原始的猜测要比上面的表述式更为精确.在高斯之后, 数学家勒让德实际上也通过数值计算得到过类似的猜测公式, 但没有高斯的精确. 证明这一结论是极其困难的工作. 直到19 世纪中叶, 切比晓夫才有了突破性进展, 他证明
C1≤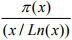 ≤C2, 这里C1, C2 是确定的常数.
≤C2, 这里C1, C2 是确定的常数.
此猜想大约到19 世纪末,才由阿达马和Paussin 几乎同时独立证明. 人们将它称作素数定理. 阿达马等人的证明是建立在天才数学家黎曼的研究基础上的,用到了极为高深的函数理论. 到了1949 年前后, 才由天才数学家艾尔多斯和塞尔伯格给出了初等证明. 请注意, 这里所谓的“初等”只是说没有用到太多高深的数学理论, 但是证明本身是很复杂的,也较为难懂. 数学中有很多这样的问题(比如哥德巴赫猜想):它们表面上很简单, 但实际上要证明它们往往是极其困难的.
素数定理只是在大样本范围内描述了一种统计规律. 素数本身的分布位置极不规则. 当你确定一个素数之后, 很难预测在它之后的下一个素数是多少.尽管如此, 我们仍有一些猜测和结论来描绘素数在整数集中分布性态. 有趣的是,猜想要比结论多得多.
首先是著名的伯特兰猜想 (后被切比晓夫证明), 它断言:
对任何大于1 的正整数n,必定有素数落在n 和2n 之间.
比如n 取4, 那么在4 到8 之间我们可以找到素数5 和7. 当n 非常大时, 这一结论显然是素数定理的直接推论.
你可以随手举出很多类似伯特兰定理的猜想, 比如在n2和(n+1)2之间是否必有素数存在? 这一看似简单的问题实际上至今仍未解决!
其次是著名的孪生素数猜想:
是否存在无限多个素数p, 使得p+2 也是素数?
我们将这样的一对素数(p,p+2)称为孪生素数对. 比如(3,5), (5,7), (11,13)等等都是孪生素数对.
类似地, 你也可以定义三生素数对 (p,p+2,p+6), 亦即要求这三个数同时为素数. 三生素数猜想就是问:是否存在无限对三生素数对?回答仍是“不知道”.我们也可以定义n 生素数对, 并提出类似的猜测. 有趣的是, 有人证明: n 生素数猜想和以下的三角不等式猜测互为矛盾—也就是说不可能同时正确!
π(x+y)≤π(x)+π(y) , 这里π(x)同前定义.
另一个著名的猜想就是在国内广为人知的哥德巴赫猜想:
任何大于等于四的偶数必定能写成两个奇素数之和; 任何大于等于9 的奇数都是三个奇素数之和.
这个猜想和陈景润的名字联系在一起, 带有很多历史的色彩. 许多民科投身于哥德巴赫猜想的证明也与此有关. 哥德巴赫只是一个普通的数学家, 除了提出这个猜想之外没有什么名气. 他将这一猜测告诉了天才数学家欧拉. 遗憾的是,后者未能证明它, 但是该猜想却得以被很多人知道. 容易看到, 哥德巴赫猜想第二部分只不过是第一部分的简单推论. 但有趣的是, 前者反而先被证明了(称作三素数定理),后者却迟迟得不到解决. 目前最好的结果是陈景润的“1+2”定理, 即
充分大的偶数都可以写成一个素数和一个殆素数之和(所谓殆素数就是说它的素因子分解中最多只有两个不同的素数).
哥德巴赫猜想的研究是十分艰难的, 它本质上涉及到十分深刻的函数论性质, 不可能如那些民科所妄想的那样, 拍拍脑袋就能用初等简单的方法做出来.
虽然我们无法彻底证实这个猜想, 但是却可以退而求其次,用所谓的密率方法得到以下的有趣结论:
任何大于1 的正整数必可写成不超过26 个素数之和.
4. 如何构造素数?
上面的讨论只是介绍了素数在整数中的分布情况, 但是我们至今还没有具体构造出这些素数来. 一个基本的问题就是:如何构造素数?
最原始的办法就是古典筛法. 比如我们要找出所有不超过100 的素数, 那么首先将所有从4 = 22开始的偶数全部从这100 个数中去除掉; 接着将所有从9 = 32开始的3 的倍数全部去除掉; 再将所有从25 = 52开始的5 的倍数全部去除掉;……以此类推, 最终通过筛选剩下的数恰好就是所有不超过100 的素数.
上面的筛法虽然可以逐一列出不超过某个上限N 的全部素数, 但是当N 很大时, 其工作量也是巨大的. 因此人们开始寻找其他方法来构造素数. 通常的思路是构造一个有规律的数列![]() , 使得数列中每一项都是素数. 这样的数列称作素数公式. 比如费马构造了以下数列(费马数), 并猜测它们都是素数:
, 使得数列中每一项都是素数. 这样的数列称作素数公式. 比如费马构造了以下数列(费马数), 并猜测它们都是素数:
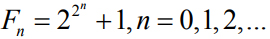
他计算了前五个,即3,5,17,257,65537,确实都是素数. 然而欧拉以其高超的计算能力手算验证了F5 = 641×6700417不是素数. 事实上, 由目前的计算机验算可知, 从F5到F11都不是素数. 是否存在无限多个费马素数?这是一个未解之谜.
尽管欧拉的计算粉碎了利用费马数构造素数公式的企图, 但是这并不表示研究费马数没有意义. 天才数学家高斯在年少时期,证明了一个让人无比惊叹的奇妙结论, 让费马素数声名大噪。这个结论(正m 边形尺规作图)是说:
一个正m 边形能用尺规作图得到的充分必要条件是:m 的所有奇素因子都是费马素数.
比如m=17 是费马素数, 因此可以用尺规作图得到正十七边形! 要知道, 在高斯之前的几百年, 有那么多人研究尺规作图问题, 但谁也没有想到正十七边形居然可以尺规作图得到。 这个结论的重要性在于, 它将几何问题和数论问题这两个看似无关的领域奇妙地结合起来.
与费马数对应的是著名的梅森数列:
Mp -1, p=2,3,5,7 …
这里p 依次取遍所有的素数. 人们也曾猜测梅森数都是素数. 比如前几项分别为3,7,31,127 都是素数. 但是M11 = 23 × 89不是素数. 一个有趣的结论断言:
如果素数p 被4 除余数为3, 并且2p+1 也是素数, 那么Mp必定不是素数.
梅森数的遭遇与费马数类似, 尽管没有能够达到原始的构造素数公式的目的, 但是它却和另一个著名的定理联系起来. 为了叙述该定理, 我们做些准备工作. 给一个正整数n, 我们把它的所有可能的因子(就是能整除n 的那些正整数)加起来得到的总和记作σ(n) . 如果n满足σ(n) = 2n , 我们就称n是完全数.比如n=6 就是完全数, 因为n 的因子只有1,2,3,6, 加起来正好是 12. 同样地, n=28 也是完全数. 我们有如下的偶完全数定理
所有的偶完全数都可以写成![]() p(p+1),这里p是梅森素数. 反之, 这样的表达式得到的数也必定是偶完全数.
p(p+1),这里p是梅森素数. 反之, 这样的表达式得到的数也必定是偶完全数.
上面说的n=6 恰好写成![]() 3(3+1),其中3 是梅森素数; 28 可以写为
3(3+1),其中3 是梅森素数; 28 可以写为![]() 7(7+1),其中7是梅森素数.
7(7+1),其中7是梅森素数.
由此产生另一个有趣的问题: 奇完全数存在吗? 这又是数论中一个至今悬而未决的著名猜想. 人们借助计算机检验了10300以内所有数,竟然都没能找到奇完全数!
欧拉提出了另一类构造素数的方式. 比如考虑多项式n2 – n + 41. 当n从0取到40 时, 多项式的值皆素数. 同样可以考虑多项式
n2 – n + p
这里p 是素数, 使得当n 从0 开始直至某个数N 为止逐一代入时,上述多项式取值始终为素数. 对任意N, 我们是否总能找到这样的p 满足上面的要求呢? 这个有趣的问题也是未解决的难题之一. 让我们在上述多项式中分别取n=1,2,3那么得到的三个值恰好为p,p+2,p+6. 如果上面的问题解决的话, 这就立刻证实了前文所述的孪生素数猜想和三生素数猜想! 因此很显然上面的问题要远远难于孪生或三生素数猜想.
看了这样几个例子之后, 你也许会问,是否真有素数公式呢?有是有的,但这类公式通常意义不大.我们这里举一个例子来说明. 为此需要一些准备. 对任何实数x, 我们用[x]表示不超过x 的最大整数. 比如[1.2]=1,[0]=0,[-1.2]=-2.这个记号是高斯引进的, 称作x 的取整函数或高斯函数. 此外我们用n!表示乘积1*2*3*…*n, 它称作n 的阶乘.
现在我们可以构造素数公式
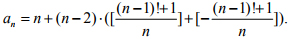
对任何大于1 的正整数n, 项an 都是素数, 比如最前面的几项分别为2, 3, 2, 5, 2, 7, …… 这个素数公式表面上看似乎很神奇, 其实并没有太多的新东西. 它只是利用了和素数有关的威尔逊定理:
一个大于1 的正整数n 是素数的充分必要条件为: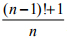 是整数.比如n=5 是素数, 4!+1=25 显然是5 的倍数.另一方面, 对任何非整数的实数x,总有[x]+[-x]=-1; 而对整数x, 则有[x]+[-x]=0. 现在我们能够看到,a_n 实际上在n 是素数时就等于n,在其他情况下都取值2.
是整数.比如n=5 是素数, 4!+1=25 显然是5 的倍数.另一方面, 对任何非整数的实数x,总有[x]+[-x]=-1; 而对整数x, 则有[x]+[-x]=0. 现在我们能够看到,a_n 实际上在n 是素数时就等于n,在其他情况下都取值2.
5. 素数和方程
素数的很多有趣味的性质都是从方程开始的. 在数论(即研究整数性质的理论)中, 人们关心的一个问题就是某些多项式方程是不是有整数解. 比如著名的勾股方程x2 + y2 = z2 , 或者佩尔方程x2 – dy2 =1等等. 当我们只关心这类方程的整数解时, 这样的方程通常就称为不定方程或者丢番图方程.
我们这里介绍一些和素数有关的方程. 它们中的一些对数学的发展起到了很大的作用. 以下设p 是素数.
(1) 我们考虑不定方程
x(x-1)…(x- (p-1)) = py.
对任一整数n,假设它被p 除的余数是r. 那么n-r 显然被p 整除. 因此对任何整数n, p 总是能整除连乘积n*(n-1)*…*(n-(p-1)) .
这样, 当我们把x=n 代入上述方程的左边, 则可求出整数解y.
(2) 费马小定理断言: 不定方程
对任何整数x=n, 都有整数解y 存在.
换句话说, 对任何整数n, 素数p总是能整除np – n. 费马小定理的“小”字是相对费马大定理(也称费马最后的定理,或者费马猜想)而言的, 他声称方程
Xn + Yn = Zn, n≥3.
没有非零的整数解(X,Y,Z) . 但费马只证明了n=4 情形. 其余情形经过许许多多数学家的艰苦努力, 终于在1994 年前后由外尔斯彻底解决.
如果我们将素数p 换成一般的整数m, 那么费马小定理可以推广到一般情形—即欧拉定理. 我们这里不打算讨论它.
(3) 假设n 是一个整数, 并且不为p 整除. 我们要求不定方程
nx – py =1
的整数解(x,y). 由费马小定理, 我们取x = np-2, 即可求得整数y. 从几何的角度看, 上面的方程在平面上描绘了一条直线. 因此我们相当于要找出该直线上的整数点(x,y).
(4)(平方剩余) 求解以下方程的整数解是初等数论的核心问题之一:
x2 – py = q
这里q 是给定的正整数. 高斯在其名著《算术研究》中对此作了深入研究,给出了一系列漂亮的研究成果. 与前面几个方程不同的是, 该方程有可能无整数解,比如
x2 – 3y = 2
如果有解, 我们就说q(在模p 下)是平方剩余的—这里不打算解释该术语的意思. 为了表示方程有无解, 勒让德引进了一个方便的符号

若p=2 的话,方程当然有解, 因此我们只关心p 是奇素数的情形. 此时高斯用巧妙的初等方法(但并不显而易见)首先得到以下结果
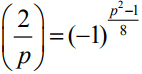
这就是说, 如果p 被8 除余数为1 或7,那么方程必定有解;否则就无解. 类似地还有
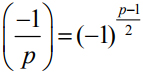
当q 也是奇素数时, 高斯发现了数论史上具有里程碑意义的重要结果,即著名的二次互反律:
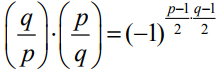
高斯将此定理比喻为“数论之酵母”, 意思是说这个深刻定理对数论的研究极其重要. 近代数学的研究也验证了这一观点. 事实上这一定理经过许多数学家—比如希尔伯特、高木贞治等—的努力,推广到代数数论研究中, 发展成了深刻的理论—类域论.
二次互反律也可以这样解释;当p,q 中有一个被4 除余数是1 时, 以下两个方程
x2 – py = q,z2 – qw = p
要么同时有解要么同时无解; 当p,q 被4 除余数都是3 时, 那么其中一个方程有解而另一方程无解.
对一般的整数q, 由算术基本定理, 我们可以将它写成素因子乘积q = ±p1 p2…ps , 从而可以通过以下关系求出勒让德符号的值以判断方程是否有解:
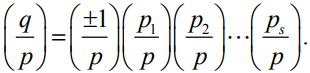
从几何角度看, 平方剩余问题对应的方程就是平面上的一条抛物线. 因此我们等价于寻找抛物线上的整数点(x,y).
(5)两平方和问题: 一个素数p 什么时候可以写成两个平方数之和? 比如
5 = 12 + 22, 13 = 22 + 32 , …
容易检验, 7 不可能写成两平方数之和. 这个问题等价于求不定方程
x2 + y2 = p.
的整数解. 从几何上看, 相当于寻找一个圆周上的整数点.
费马早在1640 年前后就得到了以下的结论, 但是并未正式发表. 欧拉最早给出了正式的证明.
如果p 被4 除余数是3,那么上述方程无解,即不能分解为两平方数之和. 如果p 被4 除余数是1, 那么方程有唯一解, 即p 能唯一地表达成两个平方数之和.
这个结论的第一部分可以从平方剩余问题(4)简单地得到. 由方程(3),我们可以找到一个整数z, 使得yz-1 能被p 整除. 因为
pz2=(xz)2+(yz)2=(xz)2+(yz-1+1)2 = (xz)2+1+ 2(yz-1)+(yz-1)2.
故
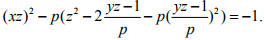
因此上面方程有解也就意味着
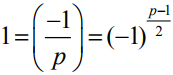
这就相当于p 被4 除余数为1.
无论如何, 要具体求出p 的平方数之和的表达式则并非易事. 这就需要用到更加高深的工具了.
上面这些不定方程研究为古典数论提供了许多重要的原动力, 发展出了很多重要的数学工具. 如何求解一般的不定方程实际上是很个困难的问题.希尔伯特在他著名的23 个数学问题中也作了探讨. 近代的一种重要思想是: 先退而求其次, 求方程的有理数解;对每个素数p, 将方程放到p-adic 数域情形去求解(p-adic 数是和素数p 有关的一类很特殊的数);我们将相应的p-adic 解综合起来,根据这些解的信息,试图构造出真正的有理数解. 这一思想曾被成功地应到二次不定方程上. 它可以归结成著名的Hasse-Minkowski定理:
假设f(x,y)是二次多项式(比如x2 + y2 -1等等), 方程f=0 有有理数解的充分必要条件是:它有实数解,并且对每个素数p, 它也有p-adic 解.
本节最后, 我们再介绍一个与素数有关的重要猜想–abc 猜想:
任意给定正实数ε > 0 , 则最多只有有限个三元组(a,b,c),满足以下条件:
(1)a,b,c 是整数, 并且两两之间互素(两个数互素,是指不存在大于1 的整数能同时整除它们)
(2)a+b=c
(3)c > d1+ε , 这里d 是abc 中所有互不相同的素因子的乘积.
如果abc 猜想正确, 那么立刻可以推出费马猜想对充分大的方幂n 都成立. 这还不止, 其实有许许多多重要的猜想和定理竟然都能从abc 猜想推出来, 而后者本身看上去却如此简单!
6.素数和代数
素数在整数中具有如此特殊的地位, 它除了包含许多有趣深刻的性质之外,也留下诸多未解之谜. 人们自然会想到将素数的概念推广到更一般的数域上来研究, 比如实数域、复数域等等.
高斯首先研究了这样一些复数(称为高斯整数):
a + b√-1,这里a,b 都取整数.所有这些复数构成的集合记为Z[√-1]. 我们可以像整数一样定义高斯整数的加减乘运算, 甚至我们还可以定义两个高斯整数的带余数除法等. 完全类似地, 我们自然也可以定义Z[√-1]中的“素数”概念.
整数集合里的素数在Z[√-1]中不一定是素数. 比如当p 被4 除余数为1 时,根据上一节的结论,它可以写成两平方数之和,
p = a2 + b2.
因此p 在Z[√-1]中可以写为两个高斯整数的乘积
p = (a + b√-1)(a – b√-1).
高斯的一项有趣的工作, 就是找出了Z[√-1]的所有素数P:
(1) P =1+ √-1;
(2) P = a + b√-1, 使得p = a2 + b2是整数集合里被4 除余数为1 的素数;
(3) P 就是整数集合里被4 除余数为3 的素数.
然后我们同样可以得到高斯整数的算术基本定理等等数论性质.
我们知道, 整数集合Z 可以扩张到有理数域Q 上—只要允许除法即可. 类似地, 高斯整数集合也可以扩张到高斯有理数域Q[√-1], 里面的数无非是两个高斯整数的商而已. 很自然地, 我们也可以考虑更一般的数域(二次域)
Q[√ m] = {a + b√m | a,b∈Q},
这里m 是任意整数, 并且我们可以假设m 不含平方因子. m=-1 就是高斯有理数域.
Q[√m]中的“整数”是什么样的呢? 答案与我们想象的稍微不同:
情形一: 如果m 被4 除余数是2 或者3, 那么二次域中的整数都可以写为
a + b√m, 这里 a,b 是整数.
情形二: 如果m 被4 除余数是1, 那么二次域中的整数可以写为
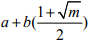 , 这里 a,b 是整数.
, 这里 a,b 是整数.
同样地, 人们可以考虑这样的整数什么时候能称作“素数”等等基本问题.那么算术基本定理在这时是否一定成立呢? 答案是否定的! 这里我们举一个简单的例子. 在Q[√-5]中, 21 竟然有两种完全不同的素因子分解:
21 = 3·7 = (1+ 2√-5)· (1- 2√-5).
在历史上,人们一开始并未意识到这一问题. 最初, 人们之所以引进这样的数域,是为了研究著名的费马猜想, 就是不定方程
Xn +Yn = Zn
没有非零整数解. 比如我们可以证明n=4 的情形没有非零的高斯整数解, 因此在整数意义下就更不可能有非零解了. 类似地, 高斯在数域Q[√-3]中也巧妙地证明了n=3 的情形也没有非零解—这一证法远比欧拉的证明更简洁且更具启发性.
一般情形下, 有人将有理数域提升到由n 次单位根生成的数域上(所谓单位根,就是方程xn =1的根).这样, 费马方程的左边在该数域下就可以分解为一次因式的乘积. 如果我们事先知道这样的数域中也有算术基本定理, 那就很容易推出矛盾,从而证明费马猜想。 当这一想法第一次被正式提出时, 遭到了很多数学家的质疑和反对. 事实上, 数学家库莫此前早已意识到这一问题, 即复数情形下“素因子”分解不一定唯一! 为了弥补这一缺陷, 库莫引入了理想数的概念, 证明理想数有类似于算术基本定理那样的唯一分解性质, 从而成功证明费马猜想在n<100 时成立 .
其实理想数并不是真正的数, 而是一组数的集合. 但有趣的是, 我们也可以定义这种集合之间的乘法运算, 并且定义出类似素数的东西—素理想, 最终证明理想数唯一分解定理—算术基本定理的推广. 理想数的引入可以说是划时代的. 它使数论的研究观点和方法产生了质的飞跃, 直接促使了代数数论的迅猛发展. 继库莫的工作之后,戴德金将理想数推广到了更一般情形, 从而发展成了系统的理想理论。 这一理论是交换代数中的核心内容之一。它不但对数论发展极为重要, 而且还深入到其他各个数学领域中, 特别是对代数几何等等学科有着重要的影响.
7.素数和函数
上一节让我们从一个侧面看到素数及算术基本定理对于数学的重要影响,它们的推广促进了代数数论等等领域的发展. 同样地,素数对与函数的研究也有极为深刻的影响.
如前所述, 除了算术基本定理, 素数另一重要的基本结论就是“素数个数无限”. 我们曾经介绍了欧几里德关于这一结论的存在性证明. 实际上,欧拉还给了另一个巧妙的证明, 这个证明极富启发性, 常被人视为解析数论之发端. 下面我们用不太严格的方式来介绍一下. 欧拉利用这样几个简单的事实:
(1)对任何介于0 和1 之间的实数x, 都有无限求和公式
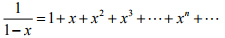
(2)将下式左边展开并利用算术基本定理得到
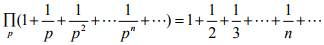
这里![]() 表示求积符号,就是把每个素数p 对应的项(1+1/p+…)都相乘起来.
表示求积符号,就是把每个素数p 对应的项(1+1/p+…)都相乘起来.
(3) 结合(1)(2), 则有
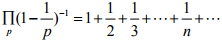
如果素数只有有限个, 那么上式左边是个有限的数. 但无论如何, 上式右边的值是无穷大 (数学上叫做”发散”), 这就推出矛盾! 因此素数个数必定无限.
我们定义一个重要的函数—黎曼ζ函数:
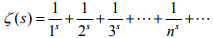
稍微推广一下前面的恒等式, 就得到有趣的恒等式
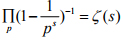
黎曼ζ函数是数学中极其重要的函数. 天才数学家黎曼首先研究了这种函数的诸多深刻性质, 并且第一次发现了黎曼ζ函数居然和素数之间存在着极为深刻的内在联系!
按照上述方式定义的的黎曼ζ 函数的定义域还比较小. 通过一定的数学技巧, 我们可以把它的定义域扩大到除了s=1 以外的整个复平面上(即对所有的不等于1 的复数s 都有定义). 人们主要关心方程
ζ(s) = 0.
这个方程的根通常称作零点. 黎曼函数有许许多多零点, 其中一部分很容易求出来, 我们把它们叫做平凡零点. 剩下那部分非平凡零点落在哪里呢? 黎曼做出了一个重要的猜测:
ζ(s)的非平凡零点一定可以写成形如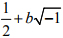 的复数(b 是实数).换言之,所有的非平凡零点都落在直线Re(s)=1/2 上, 这里Re 表示取复数的实部.
的复数(b 是实数).换言之,所有的非平凡零点都落在直线Re(s)=1/2 上, 这里Re 表示取复数的实部.
这个猜想被称为黎曼猜想, 它被列为千禧年七大数学猜想之一, 也被希尔伯特收入到23 个著名数学问题中. 这是个极其困难的问题,它远比费马猜想艰深得多. 天才数学家Degline 在特征p 的情形下证明了黎曼猜想–其实它离原始的黎曼猜想还相差很远. 尽管如此,这一杰出的工作已经影响深远,极大地促动了数学各领域的发展,特别是代数几何理论.
为什么黎曼猜想如此重要呢? 黎曼以其深刻的洞察力,发现素数的许多性质和黎曼函数的解析性质密切相关. 研究表明,许许多多重要的数论猜想或定理本质上都取决于黎曼ζ函数的非平凡零点的位置! 比如前面说的素数定理以及孪生素数猜想等等. 黎曼的这一杰出工作,可以说是开了解析数论之先河, 给数论研究提供了强有力的研究工具和技巧。
尽管我们至今无法证实黎曼猜想, 但是可以退而求其次, 想办法证明所有这些零点落在一条狭窄的区域里面–这个区域当然要包含整条直线Re(s)=1/2.我们要做的是将这个区域不断地缩小. 如果最终能压缩成直线Re(s)=1/2 那就等于证明了黎曼猜想. 一个十分有趣的现象是:区域缩得越是小,那么就能得到越多的关于素数的深刻定理.
黎曼函数也可以稍稍变化,改成更一般的狄利克雷级数
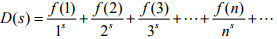
此外还有许多更复杂的函数. 数论中很大一部分问题最终都和研究这类函数的零点位置有关. 比如哥德巴赫猜想等等. 因此,从这样的深刻背景来看, 我们有理由预见, 那些表面上看似简单的未解决之难题,即使有证明也必定是极其艰深的, 绝不可能用简单的初等方法获得.
8. 小结
关于素数的故事,我们暂时讲到这里. 当然,素数还有许多重要且有趣的性质, 限于种种条件,未能一一写出来。
我个人始终觉得, 写作数学类科普文章,总是要比其他类型的文章吃力得多。原因有五:一是介绍数学需要建立在一系列概念之上,通过一环扣一环的逻辑链条方能解释清楚;二是数学往往与现实相差较远,也较抽象,很多人并不感兴趣;三是易写的数学题材也早已被人写滥; 四是很难把握好阅读对象的数学层次,也难以掌握好数学和非数学内容之间的平衡点;五是自己认为很简单很显然的东西对别人来说也许正好相反,但因“身在此山中”难以体会到读者的困惑处.
我想, 既然是数学科普,自然应该多介绍些数学,少讲些诸如“名人轶事”之类的花边材料,并且尽量限制在中学生的知识范畴之内. 但如此一来,趣味也自然大减. 若再添上公式,想必更加倒人胃口了吧. 题材选择上也一直踌躇难决……总之,自己拿起笔写科普,方才深觉其中的不易,也就越发佩服像方舟子、阿西莫夫这样的优秀科普作家. 将来必定继续努力练好文笔,希望能向世人展示数学中更多美妙之处。
写于2011年10月29日凌晨


